Lie Groups and Lie Algebras Lecture 2 notes

Smooth: of class $C^{\infty}$ (i.e. infinitely differentiable)
We want smooth manifolds because we want to work with local coordinates in our manifold like we may in $\mathbb{R}^m$. The problem is if some points belong to several charts, we have several choices for local coordinates and we want them to match/correspond.
A manifold is smooth if the transition functions between any two local coordinate systems are smooth.
That is, given two coordinate maps $\phi: V \to \mathbb{R}^m$ and $\phi': V' \to \mathbb{R}^m$, the transition function $\phi'\circ\phi^{-1}$, which takes points in $V$ to points in $V'$, should be smooth.
If $M$ is smooth, then the transition functions should be smooth.

Examples of manifolds:
- Vector space $\mathbb{R}^n$
- Any open set of $\mathbb{R}^n$
- Graph of a smooth function (map)
- Two dimensional surfaces
- Spheres $S^n$ and projective spaces $\mathbb{RP}^n$
- Lie Groups (of course)
- Homogeneous spaces of Lie groups
- Subsets in $\mathbb{R}^n$ given by a system of equations (with certain "regularity" conditions, guaranteed by implicit function theorem)

Example:
Consider the group $O(3)$ as a subset in $\mathbb{R}^9$ (3x3 matrices). The condition $\mathbf{AA}^T = \text{id}$ is a matrix equation which is equivalent to a system of 6 usual equations:

$$\begin{align*} &f_1: a_{11}^2 + a_{12}^2 + a_{13}^2 = 1 \\ &f_2: a_{11}a_{21} + a_{12}a_{22} + a_{13}a_{23} = 0 \\ &f_3: a_{11}a_{31} + a_{12}a_{32} + a_{13}a_{33} = 0 \\ &f_4: a_{21}^2 + a_{22}^2 + a_{23}^2 = 1 \\ &f_5: a_{21}a_{31} + a_{22}a_{32} + a_{23}a_{33} = 0 \\ &f_6: a_{31}^2 + a_{32}^2 + a_{33}^2 = 1 \\ \end{align*}$$

Then, if we find the jacobi matrix, we see that it's a block-triangular matrix. We see that if we add the ranks of each block, we get 6, so the matrix has rank 6. Therefore, $O(3)$ is a $9 - 6 = 3$ dimensional smooth manifold.

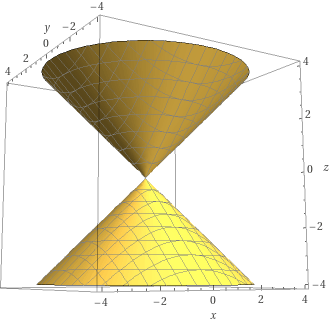
Another example:
Consider $V$, a cone, in $\mathbb{R}^3$ given by $x^2 + y^2 - z^2 = 0$.
At most points, the regularity condition $df \neq 0$ holds. But at $(0, 0, 0)$, the derivative is $0$ so the condition fails and $V$, as a whole, is not a smooth manifold.
Looking at $V$ itself, it's easy to see that $V$ isn't smooth because $(0, 0, 0)$ doesn't have a neighborhood homeomorphic to a $2$-disk.

A continuous map $F: M \to N$ between smooth manifolds is smooth if it is so in local coordinates.
More precisely, if $P \in M$ and $Q = F(P) \in N$ its image, with coordinates $(x_1, \dots, x_m)$ and $(y_1, \dots, y_n)$ in neighborhoods of $P$ and $Q$ resp, then $F$ can be written using these local coordinates:
$(y_1, \dots, y_n) = F(x_1, \dots, x_m)$, i.e. $F = (f_1(x_1, \dots, x_m), f_2(x_1, \dots, x_m), \dots, f_n(x_1, \dots, x_m))$
Smoothness of $F$ means that all $f_1, \dots, f_n$ are smooth.
Since the transition functions between charts are smooth, the above definition does not depend on the choice of local coordinates.

Tangent Vectors

In the simple sense, if we have a manifold $M$ embedded in $\mathbb{R}^n$, a tangent vector at a point $P \in M$ is just a tangent vector to a smooth curve passing through $P$.
The set of all vectors at $P$ is the tangent space to $M$ at $P$.
If we let $\gamma(t)$ be a smooth curve in $M$, i.e. a smooth map from $(-\epsilon, \epsilon) \to M$, then in local coordinates $\gamma(t) = (x_1(t), \dots, x_m(t))$.
Then, the tangent vector to gamma at point $P = \gamma(0)$ is defined to be simply $\frac{d}{dt}\gamma(0) = \left(\frac{d}{dt}x_1(0), \frac{d}{dt}x_2(0), \dots, \frac{d}{dt}x_m(0)\right)$
So, in local coordinates, any tangent vector is given as an $m$-tuple.
The problem is when we change local coordinate systems, as our function will be defined by new functions. Then, the new tangent vector in the new coordinates becomes
$\frac{d}{dt}\gamma' = \left(\frac{d}{dt}x_1', \dots, \frac{d}{dt}x_m'\right) = \left(\sum_{i=1}^m \frac{\partial}{\partial x_i} x_1' \cdot \frac{d}{dt}x_i, \dots, \sum_{i=1}^m \frac{\partial}{\partial x_i} x_m' \cdot \frac{d}{dt}x_i\right)$
Then, if the original tangent vector is $(\xi_1, \xi_2, \dots, \xi_m)$, then the same vector in the new coordinate system becomes

$$(\xi_1', \dots, \xi_m') = \left(\sum_{i=1}^m \frac{\partial}{\partial x_i} x_1'\cdot \xi_i, \dots, \sum_{i=1}^m \frac{\partial}{\partial x_i} x_m'\cdot \xi_i\right)$$