November 30 - Mini Updates

We just passed Thanksgiving, and I'm going to be a bit busy until the end of the school year, so I thought I'd write some updates while I still have a bit of time during break.

I tweeted a few days ago that I'm going to do this year's advent of code in Prolog. I meant it as a joke, but it got me looking into Prolog again - I've been doing a bunch of mini exercises, and while I'm still far from competent at it, I think I will actually do this year's advent of code in Prolog. I tried writing n-queens in Prolog and found it to be much simpler than in something like Python (which makes sense - you just have to define what a satisfactory board state looks like, and Prolog just gives it to you), so I'm pretty hopeful that I'll be able to get far. If not, my fall-back language will probably be Haskell (which I'm also trying to learn).

We just sold gamut.ink, a project I worked on two summers ago. It was a really cool opportunity I got to work on a cool idea together with my brilliant friends, and I had a lot of fun. And now that we've sold it, I got the one thing that was missing from it - closure!

One last piece of news: On December 4, I'm giving a presentation on precisely the thing I talked about in the tidbit down below.

Stay tuned!

November 8 - A Primer on Measure Theory and Ergodic Theory, leading up to Birkhoff's Ergodic Theorem

As you may know, I've been doing a DRP on Ergodic Theory for the last month and a half. I recently made a twitter post about how I thought Birkhoff's Ergodic Theorem was exceptionally cool, and I got some good feedback from my followers, so I decided I'll write an entire tidbit on some (very) basic Ergodic Theory. My goal here is to write a few paragraphs about basic ideas in Ergodic Theory, focusing on the theorems rather than the proofs. I'm assuming a very cursory knowledge of measure theory - the following will set the level of my explanation: a "measure" of a set is its "area", a set is "measurable" if it has area (most nice sets are measurable), a function is "measurable" if it only sends measurable sets to measurable sets, and a function is "measure-preserving" if the preimage of a measurable set has the same measure.

The first result we get from the above definitions is Poincaré's Recurrence Theorem. Stated simply, suppose you have some measure-preserving transformation $T: X \to X$ of a probability space (i.e. the whole space has area 1), and you take some subset $E \subset X$ with positive measure - imagine a disk or a ball or any set with "area". Then if you keep applying $T$, then almost all⁴ the points will return back to $E$ in finite time. An important caveat is that they don't always return back to $E$ at the same time; two points that are right next to each other could return to $E$ at completely different times. But they will return!⁵ This theorem blew my mind when I first came across it. You start off with only the restriction that your map has to preserve measure, and you get a result that pretty much every point in your set will loop back to the set.

Now is a good time to define ergodic maps. A map $T: X \to X$ is ergodic if the only measurable sets $B$ that satisfy $T^{-1}B = B$ have measure 0 or 1. This is the definition given in the textbook I'm using, but a nicer, equivalent definition is that $T$ is ergodic if for every pair of measurable sets $A, B$ with nonzero measure, the set $(T^{-n}A) \cap B$ has positive measure for some $n$. In layman's terms, any measurable set $B$ will have a not-insignificant chunk of it sent to any other measurable set $A$. You can think of this as a really loose kind of mixing - imagine you have a wheel and you want to rotate it by some specific angle, but you can only rotate the wheel by increments of some particular irrational angle. Of course, you won't be able to perfectly rotate your wheel to your desired angle, but you can get pretty damn close. Similarly, if you color a region of the wheel a certain color, and you color a region around the wheel another color, then after some number of rotations you're guaranteed to have those two regions overlap. Another way of thinking about it is that if you take $B$, $T^{-1}B$, $T^{-2}$, etc, and you took their union, you'd get a set of measure 1. So almost every point ends up in $B$.

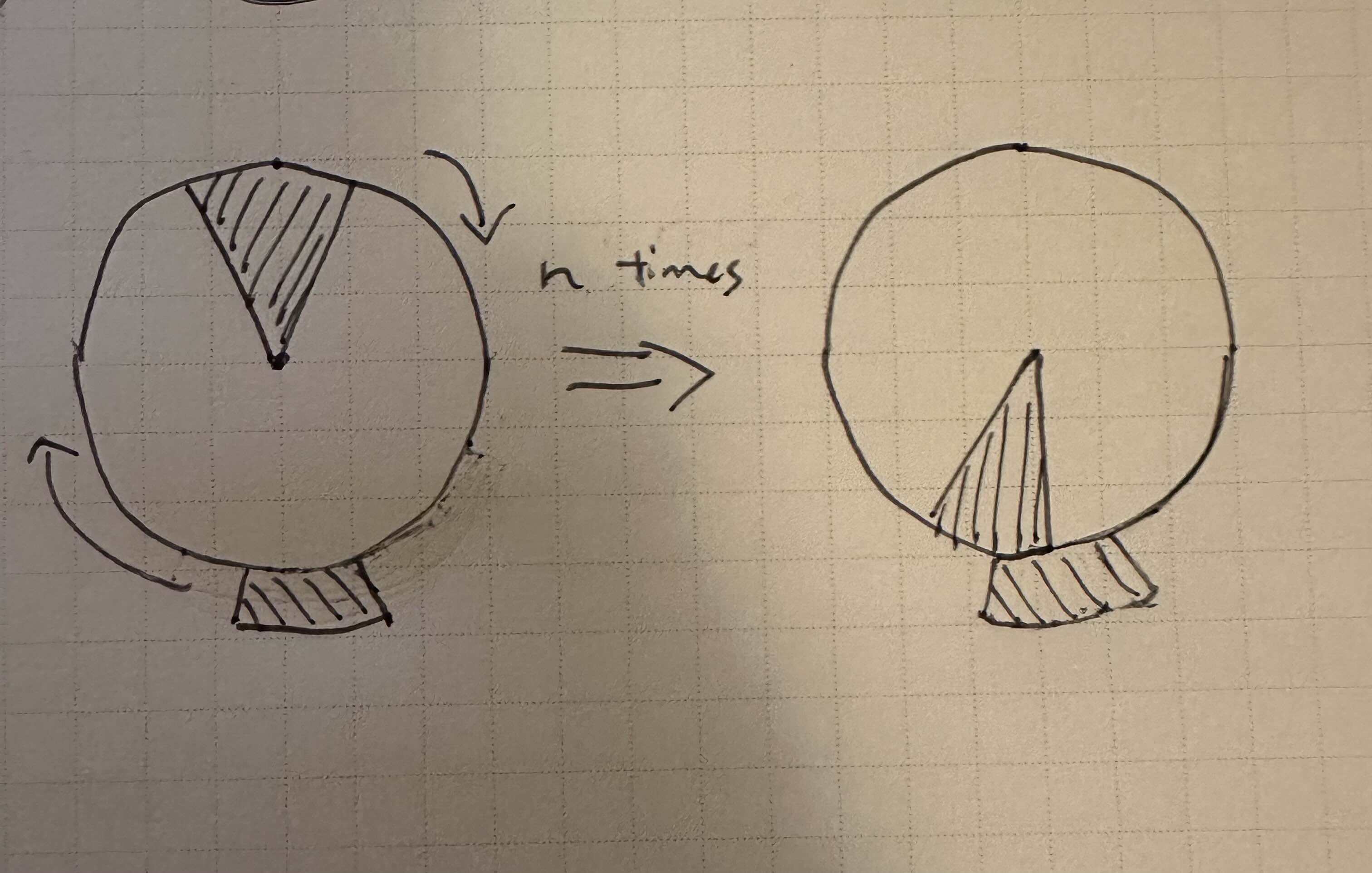
Finally, we get to talk about Birkhoff's Ergodic Theorem. Suppose we have a measurable function $f: X \to \mathbb{C}$, and a measure-preserving map $T: X \to X$. Then $(1/n)\sum_{k = 0}^{n - 1} f(T^k(x))$ converges almost everywhere to some measurable function $f^*$ with $\int f = \int f^*$. More importantly, if $T$ is ergodic, then we can imagine $T^n$ as sending $x$ to all sorts of places around $X$; so $f^*$ must be a constant almost everywhere, and we get $(1/n)\sum_{k = 0}^{n - 1} f(T^k(x)) \to \int f$. If you know of the Monte Carlo method, this might look familiar. With Monte Carlo, we take random samples from our sample space, find the value of $f$ at each of them, and then average them. In our case, we're using $T$ instead of sampling. Although $T$ isn't random, it mixes the points of $X$ up enough for it to act like it's random - at least for the purposes of taking an average. So what Birkhoff says is that the "time average" (i.e. the average of the $f(T^k(x))$ terms) is equal to the "space average" (our integral $\int f$, which we're taking across $X$).

Lastly, I'll leave you with an application. There's a cool number theory theorem that we can prove using the ergodic theorem: Borel's Theorem on Normal Numbers states that almost all numbers in $[0, 1)$, when written in binary form, have the same number of $1$'s as they do $0$'s. Here's a quick sketch of the proof. Let $T: [0, 1) \to [0, 1)$ be defined by $T(x) = 2x \mod{1}$. This map is measure-preserving and ergodic. If we let $Y$ be the set of points that have a unique binary expansion⁶, then this set has a countable complement, so the measure of $Y$ is 1. We can write any number with a unique binary expansion as $x = \sum_{i = 1}^\infty \frac{a_i}{2^i}$ for $a_i \in \{0, 1\}$; then $T(\sum_{i = 1}^\infty \frac{a_i}{2^i}) = \sum_{i = 1}^\infty \frac{a_{i + 1}}{2^i}$. Let $f(x) = 1$ if $x \in [1/2, 1)$ and $0$ otherwise. Then $f(T^n(x)) = a_{n+1}$, so $(1/n)\sum_{k = 0}^{n - 1} f(T^k(x))$ is the average number of $1$'s in the first $n$ binary digits of $x$. But we know $\lim_{n \to \infty} (1/n)\sum_{k = 0}^{n - 1}f(T^k(x)) = \int f$ almost everywhere, and $\int f = \frac{1}{2}$, so the frequency of $1$ in the binary expansion of almost every number $x \in [0, 1)$ is $\frac{1}{2}$. :)

I think this illustrates the usefulness of Ergodic Theory. Hope you learned something, or had fun reading. I'm still learning and I might not be the best at explaining things, so let me know if I made any mistakes or if I should change up the wording or if you have any questions. (Shoot, that reminds me I need a comment box or some better way to reach me. If you don't know me personally, sending me an email is probably your best bet.) Thanks for reading this!

November 1 - Updates, plan for site, some sample math

It's crazy how fast a month can go by. It's getting much more chillier in Madison (I would be so much more enthusiastic about it if my radiator worked). I wanted to write something to start off the month.

One exciting update about the site: I added footnote support to Kobo, and by extension, this site you're reading right now.¹ My vision is that these footnotes would be helpful when writing math notes. I feel like one of the main themes of math textbook discourse is bevity v.s. verbosity. A lot of people complain about textbooks saying something along the lines of "xyz follows simply from abc" when xyz doesn't follow simply from abc. This is especially the case for textbooks that are concise, like Lang's Algebra. On the other hand, if you spell out every single part of your proof you end up with really dense proofs that span multiple pages and are a pain in the ass to work through (as is the case with some of the proofs in Dummit & Foote). My proposed solution is to write the nice prose like you would see in Lang, with lots of footnotes within the prose pointing to the verbose mathematical derivation and symbolic manipulation.²

My other updates are a bit less exciting. I went to Boston to meet up with some friends and see a concert. I started reading Matsumura's Commutative Ring Theory, and I'm also planning on picking up Milnor. We've reached mixing in my Ergodic Theory DRP. My delete key on my macbook is gummy and is messing with my ability to write up pset solutions and tidbits. I started learning haskell, and I'm working through the Project Euler problems using haskell as an exercise³.

One last update: I'm going to give a talk on Category Theory sometime later this month. It's going to be an introduction to Category Theory, specifically using Ologs as a way of introducing important Category Theory concepts (like composition, functors, limits, presheafs, etc). I'll upload the slides (and maybe a recording!) once that's done. That's it for now I guess.

Footnotes